آموزش زنگ – آموزش پردازش چند مقیاسی تصاویر نجومی

اخیراً تلاش زیادی برای توسعه تکنیکهای جدید پردازش تصویر صورت گرفته است. و بسیاری از آنها از روش های پردازش سیگنال دیجیتال مانند تبدیل فوریه و موجک مشتق شده اند.
این تکنیک ها نه تنها طیف وسیعی از تکنیک های پردازش تصویر مانند کاهش نویز، شارپنینگ و گسترش دامنه پویا را فعال کرده اند، بلکه بسیاری از تکنیک های مورد استفاده در بینایی محاسباتی مانند تشخیص لبه، تشخیص اشیا و غیره را نیز فعال کرده اند.
تجزیه و تحلیل چند مقیاسی یکی از تکنیک های جدیدتر (به طور نسبی) است که در طیف گسترده ای از کاربردها، به ویژه در کاربردهای نجومی و پردازش داده ها به کار گرفته شده است. این تکنیک، که بر اساس تبدیل موجک است، به ما امکان می دهد داده های خود را به چندین سیگنال تقسیم کنیم، که همه آنها برای ایجاد سیگنال نهایی جمع می شوند.
سپس میتوانیم کار پردازش یا تحلیل خود را بر روی این سیگنالهای فرعی انجام دهیم و به ما امکان میدهد تا عملیات هدفمندی را انجام دهیم که تأثیری بر سیگنالهای فرعی دیگر ندارد.
در این آموزش، ابتدا از طریق لنز یک الگوریتم خاص برای انجام تجزیه و تحلیل چند مقیاسی روی تصاویر، به تحلیل این تکنیک خواهیم پرداخت. سپس به تحلیل چگونگی پیاده سازی آنچه در قسمت اول در زبان برنامه نویسی Rust پرداختیم می پردازیم و نمونه هایی را که در نیمه اول مقاله می بینید بازسازی می کنیم.
قبل از اینکه بخوانی:
پیش نیازهای قسمت 1:
تکنیک توصیف شده از مفهوم "تبدیل موجک" مشتق شده است. لازم نیست همه چیز را در مورد آن بدانید، اما یک درک بسیار ابتدایی به شما کمک می کند تا مطالب را بهتر درک کنید.
از آنجایی که مقاله بر پردازش و تجزیه و تحلیل تصویر تمرکز دارد، درک اولیه از نحوه عملکرد پیکسل ها در فرمت دیجیتال مفید است، اما اجباری نیست.
پیش نیازهای قسمت 2:
در اینجا، ما بر پیاده سازی الگوریتم با استفاده از زبان برنامه نویسی Rust تمرکز می کنیم، بدون اینکه وارد جزئیات خود زبان شویم. پس نوشتن برنامه های Rust و خواندن راحت اسناد جعبه مورد نیاز است.
اگر این شما نیستید، همچنان میتوانید قسمت 1 را بخوانید و این تکنیک را یاد بگیرید، و سپس شاید بخواهید آن را به زبان دلخواه خود امتحان کنید. اگر با Rust آشنایی ندارید، به شدت شما را به یادگیری اصول اولیه تشویق می کنم. در اینجا یک دوره تعاملی Rust آمده است که می تواند شما را شروع کند.
فهرست مطالب
بخش 1: درک تکنیک و الگوریتم پردازش چند مقیاسی
قسمت 2: نحوه پیاده سازی À Trous Tranform در Rust
Iterators And The Trous Transform
با استفاده از À Trous Transform
بخش 1: درک تکنیک و الگوریتم پردازش چند مقیاسی
پس وقتی از پردازش یا تجزیه و تحلیل چند مقیاسی برخی داده ها صحبت می کنیم، منظورمان چیست؟ خوب، منظور ما معمولاً شکستن داده های ورودی به سیگنال های متعدد است که هر یک مقیاس خاصی از اطلاعات را نشان می دهد.
مقیاس، زمانی که در مورد تجزیه و تحلیل تصویر صحبت می کنیم، به سادگی به اندازه ساختارهایی که در هر زمان به آنها نگاه می کنیم اشاره دارد. هر چیز دیگری را که کوچکتر یا بزرگتر از مقیاس فعلی است نادیده می گیرد.
پردازش تصویر چند مقیاسی چیست؟
برای تصاویر، "مقیاس" به طور کلی به اندازه در پیکسل ساختارهای مختلف یا جزئیات در تصویر اشاره دارد. با نگاه کردن به مثال زیر می توانید به درک شهودی دست یابید:

با فرض اینکه درک ساده ما درست باشد، می توانیم تصاویری از حداقل 3 مقیاس زیر استخراج کنیم:
ساختارهای بسیار کوچک، معمولاً به اندازه یک پیکسل. این لایه، وقتی از بقیه تصویر جدا میشود، در بیشتر قسمتها فقط حاوی نویز و تعدادی ستاره تیز است.
ساختارهای کوچک، معمولاً در اندازه چند پیکسل. این لایه، وقتی جدا شود، حاوی تمام ستارگان و جزئیات بسیار ظریف بازوهای کهکشان خواهد بود.
ساختارهای در مقیاس بزرگ و بسیار بزرگ، معمولاً 100 پیکسل در اندازه. این لایه، وقتی جدا شود، اندازه و شکل کلی کهکشان را در مرکز خواهد داشت.
حال این سوال پیش میآید که چرا در وهله اول باید همه این کارها را انجام دهیم؟
پاسخ ساده است: به ما این امکان را می دهد که بهبودها و تغییرات هدفمند را در یک تصویر ایجاد کنیم.
به عنوان مثال، کاهش نویز در تصویر کلی معمولا منجر به از دست دادن وضوح در کهکشان می شود. اما از آنجایی که ما تصویر خود را به مقیاسهای متعدد تقسیم کردهایم، به راحتی میتوانیم کاهش نویز را فقط در چند لایه اول اعمال کنیم، زیرا بیشتر نویز تصادفی که به راحتی حذف میشود، فقط در لایههای مقیاس پایینتر قرار دارد.
سپس لایههای کممقیاس کاهشیافته را با لایههای در مقیاس بزرگ اصلاح نشده ترکیب میکنیم و خروجیای داریم که بدون افت کیفیت، نویز را کاهش میدهد.
نکته عجیب دیگر در مورد نویز این است که تقریباً همیشه فقط در یکی از این لایهها وجود دارد و فرآیند کاهش نویز را هم آسان و هم غیرمخرب میکند.
اگر بیشتر یک یادگیرنده بصری هستید، بیایید این را در عمل با استفاده از تصویری که در بالا استفاده کردیم، ببینیم. ما با نسخه خاکستری زیر از آن تصویر کار خواهیم کرد، که در آن نویز گاوسی تصادفی را نیز اضافه کرده ام:

با انجام جداسازی لایه های مبتنی بر مقیاس در این تصویر، نتایج زیر را دریافت می کنیم. توجه داشته باشید که نتایج به محدوده ای تغییر مقیاس داده می شوند که می توان آنها را به عنوان یک تصویر برای اهداف نمایشی مشاهده کرد. تبدیل واقعی مقادیر پیکسلی را تولید میکند که وقتی مستقل به آنها نگاه میشود، معنی ندارند، اما همه تکنیکها و محاسباتی که در این آموزش توضیح داده شدهاند، همچنان میتوانند با خیال راحت و بدون تغییر مقیاس اعمال شوند. فرآیند ترکیب مجدد به طور خودکار محدوده صحیح را به ما برمی گرداند:









لایه اول و دوم حاوی نویز و ستاره است. در این مثال خاص، نویز با ستاره ها مخلوط شده است. اما با استفاده از لایههای اول و دوم، میتوانیم به راحتی مناطقی را که در لایه دوم وجود ندارد، هدف قرار دهیم، زیرا میتوانیم مطمئن باشیم که در آنها نویز در لایه اول وجود دارد.
با لایه سوم، همچنان درخشندگی باقیمانده از ستاره ها را می بینیم. اما اگر به دقت نگاه کنید، بازوهای کهکشان را نیز بسیار کم رنگ می بینیم که شروع به ظاهر شدن می کنند.
از لایه چهارم به بعد، ما کهکشان را در مقیاس ها و سطوح جزئیات متفاوت، کاملاً بدون ستاره ها می بینیم. ما با جزئیات ریزتر (جزئیات در مقیاس نسبتا کوچک) شروع می کنیم و به طور فزاینده ای به سمت نمونه های بزرگتر و بزرگتر می رویم. در پایان، ما فقط یک شکل مبهم را در جایی که کهکشان در گذشته مشاهده می کنیم.
از اینجا به بعد، می توانیم به طور انتخابی کاهش نویز را در دو لایه اول اعمال کنیم. سپس میتوانیم همه لایهها را دوباره ترکیب کنیم تا تصویر زیر را ایجاد کنیم که نویز بسیار کمی دارد و در عین حال همان مقدار جزئیات را در ستارگان و بازوهای کهکشان حفظ میکند:

در ابتدایی ترین شکل آن، تجزیه و تحلیل چند مقیاسی شامل تقسیم تصویر منبع شما، که معمولاً به آن "سیگنال" می گویند، به چندین "سیگنال" - که هر کدام حاوی داده های مقیاس خاصی در سیگنال منبع است، می شود.
مقیاس، زمانی که در اینجا در مورد سیگنال تصویر صحبت می کنیم، به فاصله بین پیکسل های مجاور که هنگام ایجاد لایه از تصویر منبع می گیریم، اشاره دارد.
در عمل، این تکنیک به عنوان یکی از اولین گام ها در انواع تجزیه و تحلیل داده های نجومی و پردازش تصویر استفاده می شود.
به عنوان مثال، میتوانید از این تکنیک برای شناسایی مکانهای ستارهها استفاده کنید، در حالی که ساختارهای بزرگتر را خیلی راحتتر از آنچه در غیر این صورت ممکن است نادیده میگیرید.
تبدیل موجک À Trous
همه چیزهایی که قبلاً به شما نشان دادم، و همه چیزهایی که قرار است در این آموزش ببینید، با تجزیه موجک و ترکیب مجدد با استفاده از الگوریتم à trous برای تبدیل موجک گسسته به دست آمد.
این الگوریتم در طول سال ها برای کاربردهای مختلف مورد استفاده قرار گرفته است. اما اخیراً در کاربردهای پردازش تصویر نجومی اهمیت ویژهای پیدا کرده است، جایی که اشیاء و سیگنالهای مختلف در یک تصویر را میتوان بر اساس مقیاسهای ساختاری کاملاً از هم جدا کرد.
در اینجا نحوه کار الگوریتم آمده است:
ما با ورودی تصویر منبع و تعداد سطوح شروع می کنیم تا به n تجزیه شود.
برای هر سطح n:
ما تصویر را با تابع مقیاسبندی خود در هم میکشیم (کمی خواهیم دید که این چیست)، که در آن پیکسلهای مجاور به اندازه 2 n واحد از یکدیگر در نظر گرفته میشوند که نتیجه n را به ما میدهد. از اینجا نام "À Trous" می آید که به معنای واقعی کلمه به "با سوراخ" ترجمه می شود.
سپس خروجی لایه n با استفاده از ورودی - نتیجه n محاسبه می شود.
سپس ورودی را به نتیجه مساوی n به روز می کنیم. این همچنین به عنوان داده باقی مانده شناخته می شود که به عنوان داده منبع برای لایه بعدی عمل می کند.
مراحل بالا را برای تمام سطوح تکرار کنید.
در نهایت 9 لایه موجک و 1 لایه باقیمانده داریم. همه 10 لایه برای ترکیب مجدد مورد نیاز است.
برای یک رویکرد ریاضی بیشتر برای درک این الگوریتم، من شما را تشویق می کنم که در مورد الگوریتم à trous اینجا بخوانید .
فرآیند ترکیب مجدد بسیار ساده است: فقط باید هر 10 لایه را با هم اضافه کنیم. میتوانیم بایاس مثبت یا منفی را برای هر یک از لایهها اعمال کنیم، که عاملی برای ضرب کردن مقادیر پیکسل لایه در طول ترکیب مجدد است. می توانید از آن برای افزایش یا کاهش ویژگی های آن لایه خاص استفاده کنید.
توابع مقیاس بندی
توابع مقیاسبندی، هستههای پیچشی خاصی هستند که به ما کمک میکنند دادهها را در مقیاسی خاص بر اساس مورد استفاده خود بهتر نمایش دهیم. 3 توابع مقیاس بندی متداول وجود دارد که در زیر نشان داده شده است:



B3 Spline یک هسته بسیار روان است. بیشتر در جداسازی سازه های مقیاس بزرگ استفاده می شود. اگر می خواستیم کهکشان خود را تیز کنیم، از این هسته استفاده می کردیم.
مقیاس پایین یک هسته بسیار تیز است و در کار با ساختارهای مقیاس کوچک بهترین است.
هسته درونیابی خطی بهترین هر دو جهان را به ما می دهد، و از این رو زمانی استفاده می شود که ما نیاز به کار با ساختارهای مقیاس کوچک و مقیاس بزرگ داریم. این همان چیزی است که ما در تمام نمونه های قبلی خود استفاده کرده ایم.
پیکسل های پیچیدگی در هر مقیاس
در الگوریتم اشاره کردم که در هر مقیاس، پیکسل های تصویر 2 n واحد از هم فاصله دارند. بیایید سعی کنیم با استفاده از تجسم زیر درک بهتری از این موضوع داشته باشیم:
تصویر 8 پیکسل در 8 پیکسل زیر را در نظر بگیرید. هر پیکسل دارای برچسب 1 تا 64 است که شاخص آنها است.
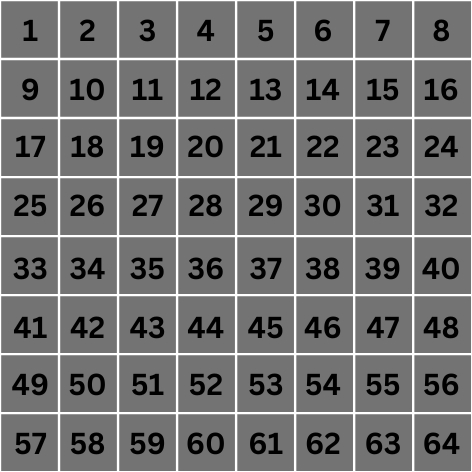
ما فقط برای این مثال بر روی عملیات کانولوشن یکی از پیکسل های مرکزی تمرکز می کنیم، مثلا پیکسل شماره 28.
مقیاس 0: در مقیاس 0، مقدار 2 n تبدیل به 1 می شود. این بدان معنی است که برای کانولوشن، پیکسل هایی را در نظر می گیریم که 1 واحد از پیکسل مرکز هدف ما فاصله دارند. این پیکسل ها در زیر مشخص شده اند:
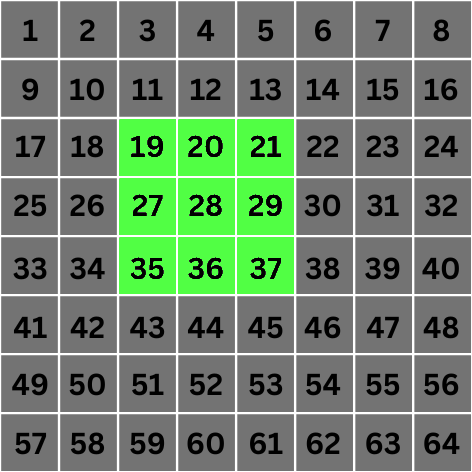
مقیاس 1: اینجاست که همه چیز جالب می شود. در مقیاس 1، مقدار 2 n تبدیل به 2 می شود. این بدان معناست که برای کانولوشن، مستقیماً به پیکسلهایی میرویم که 2 مکان از پیکسل هدف فاصله دارند:
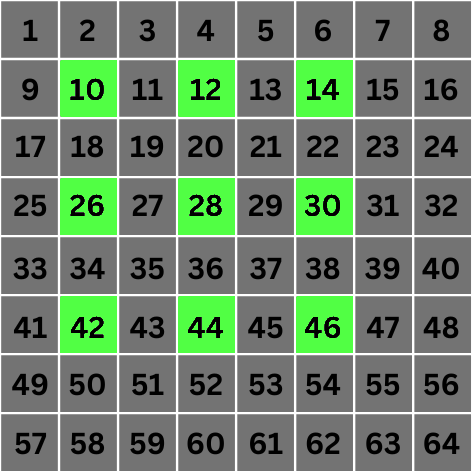
همانطور که می بینید، ما با پرش از 2 n - 1 پیکسل مجاور و انتخاب پیکسل 2 n ام ، "حفره هایی" را در محاسبه مقدار پیکسل هدف ایجاد کرده ایم. این اساس الگوریتم است.
این فرآیند برای هر پیکسل در تصویر تکرار می شود، درست مانند یک فرآیند کانولوشن معمولی. و هر بار برای محاسبه مقادیر نهایی در مقیاس های افزایشی، فاصله بین پیکسل ها را افزایش می دهیم.
بیایید فقط به یک مقیاس دیگر نگاه کنیم.
مقیاس 2 : اینجاست که همه چیز جالب تر می شود. در مقیاس 2 مقدار 2 n می شود 4 . این بدان معناست که برای کانولوشن، مستقیماً به پیکسلهایی میرویم که 4 مکان از پیکسل هدف فاصله دارند:
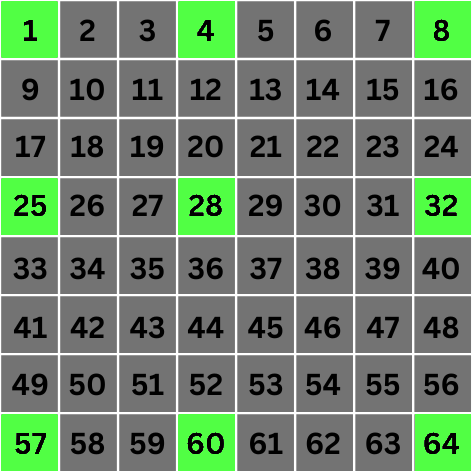
صبر کن چی؟ چرا پیکسل های 1، 4، 8، 25 و 57 را انتخاب می کنیم؟ 1 و 4 فقط 3 مکان از هم فاصله دارند، 25 فقط 2 مکان از هم فاصله دارند، و 8 و 57 حتی به صورت مورب با پیکسل هدف هم تراز نیستند. چه خبر است؟
رسیدگی به شرایط مرزی
همانطور که اشاره کردیم که این فرآیند برای همه پیکسلهای یک تصویر اجرا میشود، باید مواردی را نیز در نظر بگیریم که مکانهای پیکسل برای کانولوشن خارج از تصویر قرار دارند.
این یک مفهوم منحصر به فرد برای این الگوریتم نیست. در حین کانولوشن، به این شرایط مرزی یا کنترل پیکسل های مرزی گفته می شود. تکنیکهای مختلفی برای مقابله با این موضوع وجود دارد، و همه آنها شامل گسترش مجازی تصویر است تا به نظر برسد که ما اصلاً با مرز مواجه نیستیم.
برخی از تکنیک ها عبارتند از:
با کپی کردن مقدار آخرین سطر/ستون، به اندازه نیاز گسترش مییابد
انعکاس تصویر در تمام لبه ها و گوشه ها
پیچیدن تصویر در اطراف لبه ها.
در مثال خود، ما از تکنیک "آینه سازی" استفاده می کنیم. هنگام اجرای چنین الگوریتمی، نیازی به ایجاد یک تصویر توسعه یافته نداریم. هر پردازش مرزی فقط با استفاده از فرمول های ریاضی پایه قابل پیاده سازی است.
تصویر توسعه یافته ما، با پیکسل های صحیح انتخاب شده برای مقیاس 2، به شرح زیر است:

باز هم، پسوند فقط منطقی است و به طور کامل با استفاده از فرمول ها محاسبه می شود، برخلاف اینکه در واقع تصویر منبع را گسترش داده و سپس تحلیل کنید. ما به راحتی میتوانیم ببینیم که با وجود تصاویر آینهای، قانون اساسی ما برای انتخاب پیکسلهایی که 2 n مکان از هم فاصله دارند، همچنان رعایت میشود.
محاسبه حداکثر مقیاس های ممکن برای هر تصویر داده شده
اگر با دقت در مورد آن فکر کنید، خواهید دید که حداکثر لایه هایی که یک تصویر می تواند به آنها تجزیه شود را می توان با محاسبه log 2 عرض یا ارتفاع تصویر (هر کدام کمتر باشد) و دور انداختن قسمت کسری محاسبه کرد.
در تصویر 5x5 ما، log 2 (5) ~= 2.32 . اگر قسمت کسری را دور بیندازیم، 2 لایه باقی می ماند. به طور مشابه، برای یک تصویر 1000x1000 پیکسل، log 2 1000 ~= 9.96 ، یعنی ما می توانیم یک تصویر 1000x1000 پیکسل را به حداکثر 9 لایه تجزیه کنیم. این به سادگی نشان می دهد که "سوراخ" ما نمی تواند بزرگتر از عرض یا ارتفاع باشد.
حتی با پسوند آینهای که در بالا استفاده کردیم، اگر حفرهها بزرگتر از عرض تصویر باشند، همچنان به خارج از مناطق توسعهیافته ختم میشوند، بهویژه برای پیکسلهای گوشهای یا مرزی که انجام کانولوشن در آن مقیاس را غیرممکن میکند.
یادداشت های پایانی
اگر کمی بیشتر به مثالها و تجسمها فکر کنید، میتوانید به وضوح ببینید که این الگوریتم چگونه و چرا کار میکند و چگونه میتواند ساختارها را در یک تصویر بر اساس اندازههایشان جدا کند. افزایش اندازه سوراخ ها باعث می شود که فقط ساختارهای بزرگتر از خود سوراخ برای هر لایه معین حفظ شوند.
مزیت بزرگ استفاده از این الگوریتم هزینه محاسباتی است. از آنجایی که این شامل تبدیل فوریه یا موجک نیست، هزینه محاسباتی نسبتاً کم است. با این حال، هزینه حافظه در واقع بالاتر است. اما اغلب این یک معامله خوب است.
یکی دیگر از مزایای این الگوریتم در مقایسه با سایر الگوریتم های تبدیل موجک گسسته این است که اندازه تصویر منبع در کل فرآیند حفظ می شود. در اینجا هیچ گونه تخریب یا ارتقاء مقیاسی اتفاق نمی افتد، و این الگوریتم را به یکی از ساده ترین الگوریتم ها برای درک و پیاده سازی تبدیل می کند.
این الگوریتم تقریباً در تمام نرم افزارهای پردازش تصویر نجومی مانند PixInsight ، Siril و بسیاری دیگر استفاده می شود.
این الگوریتم با نام های دیگری مانند Stationary Wavelet Transform و Starlet Transform نیز شناخته می شود.
قسمت 2: نحوه پیاده سازی À Trous Tranform در Rust
اکنون قصد دارم به شما نشان دهم که چگونه می توانید این الگوریتم را در Rust پیاده سازی کنید.
برای اهداف این آموزش، میخواهم فرض کنم که شما با Rust و مفاهیم اولیه آن، مانند انواع دادهها، تکرارکنندهها و ویژگیها کاملاً آشنا هستید و برنامههایی را راحت مینویسید که از این مفاهیم استفاده میکنند.
من همچنین میخواهم فرض کنم که شما درک درستی از مفهوم کانولوشن و کرنلهای کانولوشن در این زمینه دارید.
پیش نیازها
ما به چند وابستگی نیاز خواهیم داشت. قبل از رسیدن به آن، اجازه دهید به سرعت یک پروژه جدید ایجاد کنیم:
cargo new --lib atrous-rs cd atrous-rsحالا بیایید تمام وابستگی هایی که نیاز داریم را تحلیل کنیم. ما در واقع فقط به 2 مورد نیاز داریم:
cargo add image ndarray image یک کتابخانه Rust است که از آن برای کار با تصاویر همه فرمتها و کدگذاریهای استاندارد استفاده میکنیم. همچنین به ما کمک می کند تا بین فرمت های مختلف تبدیل کنیم و دسترسی آسان به داده های پیکسل را به عنوان بافر فراهم می کند.
ndarray یک کتابخانه Rust است که به شما کمک می کند آرایه های 2 بعدی، 3 بعدی یا N-Dimensional را ایجاد، دستکاری و کار کنید. ما میتوانیم از بردارهای تودرتو استفاده کنیم، اما استفاده از پروژهای مانند ndarray در این مورد بهتر است زیرا باید عملیات زیادی را هم روی مقادیر فردی و هم بر روی همسایههای آنها انجام دهیم. نه تنها انجام آن با ndarray بسیار ساده تر است، اما آنها همچنین دارای بهینه سازی عملکرد برای بسیاری از عملیات ها و انواع CPU هستند.
اگرچه من توابع/ویژگی ها/روش ها/انواع داده ای که از این جعبه ها استفاده می کنیم را پوشش خواهم داد، اما قصد ندارم به جزئیات زیاد آنها بپردازم. من به شما توصیه می کنم به جای آن اسناد را بخوانید.
ما در واقع مستقیماً به پیاده سازی الگوریتم می رویم و بعداً برمی گردیم تا ببینیم چگونه می توانیم از آن استفاده کنیم.
تبدیل À Trous
یک فایل جدید ایجاد کنید که اجرای ما را نگه می دارد. بیایید نام آن را transform.rs بگذاریم.
با گفت ن ساختار زیر شروع کنید، که اطلاعات مورد نیاز برای انجام تبدیل را در خود نگه می دارد:
// transform.rs use ndarray::Array2; pub struct ATrousTransform { input: Array2<f32>, // `Array2<f32>` is a 2D array where each value is of type `f32`. This will hold our pixel data for input image. levels: usize, // The number of levels or scales to decompose the image into current_level: usize, // Current level that we need to generate. This holds the state of our iterator. width: usize, // Width of input image height: usize, // Height of input image }ما همچنین به راهی برای ایجاد آسان این ساختار نیاز داریم. در مورد ما، میخواهیم بتوانیم آن را مستقیماً از تصویر ورودی ایجاد کنیم. همچنین، تصویر ورودی میتواند از هر یک از فرمتها و کدگذاری پشتیبانیشده باشد، اما ما میخواهیم یک نوع رنگ ثابت برای اجرای محاسبات داشته باشیم، پس باید تصویر را به فرمت مورد انتظار خود تبدیل کنیم.
استخراج همه این منطق با استفاده از الگوی "سازنده" در Rust مفید است. بیایید آن را اجرا کنیم:
// transform.rs use image::GenericImageView; impl ATrousTransform { pub fn new(input: &image::DynamicImage, levels: usize) -> Self { let (width, height) = input.dimensions(); let (width, height) = (width as usize, height as usize); // Create a new 2D array with proper size for each dimension to hold all of our input's pixel data. Method `zeros` takes a "shape" parameter, which is a tuple of (rows_count, columns_count). let mut data = Array2::<f32>::zeros((height, width)); // Convert the image to be a grayscale image where each pixel value is of type `f32`. Loop over all pixels in the input image along with its 2D location. for (x, y, pixel) in input.to_luma32f().enumerate_pixels() { // Put the pixel value at appropriate location in our data array. The `[[]]` syntax is used to provide a 2-dimensional index such as `[[row_index, col_index]]` data[[y as usize, x as usize]] = pixel.0[0]; } Self { input: data, levels, current_level: 0, width, height } } } این کار به تبدیل تصویر به مقیاس خاکستری و تبدیل مقادیر پیکسل به f32 کمک می کند. اگر از قبل آگاه نیستید، برای تصاویر با مقادیر پیکسل ممیز شناور، مقادیر همیشه نرمال می شوند. این بدان معنی است که آنها همیشه بین 0 و 1 - 0 نشان دهنده سیاه و 1 نشان دهنده سفید هستند.
Iterators و À Trous Transform
قبل از اینکه ادامه دهیم، بیایید یک ثانیه در مورد الگوریتم فکر کنیم. ما باید بتوانیم تصاویر را در مقیاس های فزاینده تولید کنیم، تا زمانی که به حداکثر تعداد سطوح مورد نیاز خود برسیم.
ما میخواهیم مصرفکننده کتابخانه ما به همه این مقیاسها دسترسی داشته باشد و بتواند آنها را دستکاری کند و همچنین پس از اتمام آنها به راحتی دوباره ترکیب شود. آنها باید بتوانند لایه ها را فیلتر کنند تا ساختارها را در مقیاس های خاص نادیده بگیرند، آنها را دستکاری یا "نقشه برداری" کنند تا ویژگی های آنها را تغییر دهند، عملیاتی را روی آنها انجام دهند یا حتی در صورت نیاز هر تصویر را ذخیره کنند.
این خیلی شبیه به تکرار کننده هاست! تکرار کننده ها متدهایی مانند filter ، skip ، take ، map ، for_each و غیره را در اختیار ما قرار می دهند که همه اینها دقیقاً تمام آن چیزی است که ما برای کار با لایه های خود قبل از ترکیب مجدد نیاز داریم.
یکی از مزیت های اضافه شده Iterators این است که به شما امکان می دهد قبل از اینکه به لایه بعدی بروید، پردازش هر لایه را تا آخر تمام کنید. اگر مطمئن نیستید که چرا چنین است، پیشنهاد میکنم درباره پردازش یک سری موارد با Iterators در Rust بیشتر بخوانید.
ما صفت Iterator برای نوع ATrousTransform خود پیاده سازی می کنیم که باید یک لایه موجک به عنوان خروجی برای هر تکرار تولید کند.
ما ابتدا قسمتهای داخلی الگوریتم را پیادهسازی میکنیم و از آنجا میسازیم. پس ما ابتدا به راهی نیاز داریم که یک بافر داده ورودی را با تابع مقیاسبندی در هم بپیچیم و در عین حال مطمئن شویم که پیکسلهای مجاور 2 n مکان از هم فاصله دارند، که اولین گام در حلقه ما است.
پیچیدگی
قبل از اینکه بتوانیم کاری انجام دهیم، باید هسته کانولوشن خود را تعریف کنیم. یک فایل جدید kernel.rs ایجاد کنید و آن را با محتوای زیر به lib.rs اضافه کنید:
// kernel.rs #[derive(Copy, Clone)] pub struct LinearInterpolationKernel { values: [[f32; 3]; 3] } impl Default for LinearInterpolationKernel { fn default() -> Self { Self { values: [ [1. / 16., 1. / 8., 1. / 16.], [1. / 8., 1. / 4., 1. / 8.], [1. / 16., 1. / 8., 1. / 16.], ] } } }ما آن را با استفاده از یک ساختار به جای یک آرایه ثابت از آرایه ها تعریف می کنیم، زیرا باید چند روش مفید کوچک روی آن تعریف کنیم که مربوط به مدیریت شاخص هستند. بعداً به آن باز خواهیم گشت.
یک فایل convolve.rs دیگر ایجاد کنید. این جایی است که تمام کدهای مربوط به کنترل کانولوشن برای تک تک پیکسل ها قرار می گیرد. ما یک ویژگی Convolution را تعریف می کنیم که روش های مورد نیاز برای انجام کانولوشن روی هر پیکسل در لایه فعلی را تعریف می کند.
// convolve.rs pub trait Convolution { fn compute_pixel_index( &self, distance: usize, kernel_index: [isize; 2], target_pixel_index: [usize; 2] ) -> [usize; 2]; fn compute_convoluted_pixel( &self, distance: usize, index: [usize; 2] ) -> f32; } ممکن است بپرسید چرا به جای یک بلوک ساده impl به یک ویژگی در اینجا نیاز داریم. ما در این مقاله فقط با تصاویر Grayscale کار می کنیم، اما ممکن است بخواهید آن را گسترش دهید تا آن را برای RGB یا سایر حالت های رنگی نیز اجرا کنید.
اکنون، شما باید این ویژگی را برای ساختار ATrousTransform خود پیاده سازی کنید:
// convolve.rs impl Convolution for ATrousTransform { fn compute_pixel_index( &self, distance: usize, kernel_index: [isize; 2], target_pixel_index: [usize; 2] ) -> [usize; 2] { let [kernel_index_x, kernel_index_y] = kernel_index; // Compute the actual distance of adjacent pixel // by multiplying their relative position with the // size of the hole. let x_distance = kernel_index_x * distance as isize; let y_distance = kernel_index_y * distance as isize; let [x, y] = target_pixel_index; // Compute the index of adjacent pixel in the 2D // image based on the index of current pixel. let mut x = x as isize + x_distance; let mut y = y as isize + y_distance; // If x index is out of bounds, consider x to be // the nearest boundary location if x < 0 { x = 0; } else if x > self.width as isize - 1 { x = self.width as isize - 1; } // If y index is out of bounds, consider y to be // the nearest boundary location if y < 0 { y = 0; } else if y > self.height as isize - 1 { y = self.height as isize - 1; } // The final 2D index of pixel. [y as usize, x as usize] } fn compute_convoluted_pixel( &self, distance: usize, [x, y]: [usize; 2] ) -> f32 { // Create new variable to hold the result of convolution // for current pixel. let mut pixels_sum = 0.0; let kernel = LinearInterpolationKernel::default(); // Iterate over relative position of pixels from the center // pixel to perform convolution with. In other words, // these are the indexes of neighbouring pixels from the // center pixel. for kernel_index_x in -1..=1 { for kernel_index_y in -1..=1 { // Get the computed pixel location that maps to // the current position in kernel let pixel_index = self.compute_pixel_index( distance, [kernel_index_x, kernel_index_y], [x, y] ); // Get the multiplicative factor (kernel value) for // this relative location from the kernel. let kernel_value = kernel.value_from_relative_index( kernel_index_x, kernel_index_y ); // Multiply the pixel value with kernel scaling // factor and add it to the pixel sum. pixels_sum += kernel_value * self.input[pixel_index]; } } // Return the value of computed pixel from convolution process. pixels_sum } }ما باید محاسباتی را انجام دهیم تا مکان هر پیکسل را بر اساس موقعیت نسبی هسته از پیکسل مرکزی تعیین کنیم و همچنین اطمینان حاصل کنیم که "اندازه سوراخ" نیز برای شاخص نهایی پیکسل در نظر گرفته شده است. همانطور که ممکن است متوجه شوید، شما همچنین می خواهید شرایط مرزی را هنگام محاسبه شاخص ها کنترل کنید.
پیشنهاد می کنم وقت خود را در اینجا صرف کنید و کد و نظرات را مرور کنید.
پیاده سازی Iterator
بالاخره زمان اجرای ویژگی Iterator برای ATrousTransform فرا رسیده است:
// transform.rs impl Iterator for ATrousTransform { // Our output is an image as well as the current level for each // iteration. The current level is an `Option` to represent the // final residue layer after the intermediary layers have been // generated. type Item = (Array2::<f32>, Option<usize>); fn next(&mut self) -> Option<Self::Item> { let pixel_scale = self.current_level; self.current_level += 1; // We've already generated all the layers. Return None to // exit the iterator. if pixel_scale > self.levels { return None; } // We've generated all intermediary layers, return the // residue layer. if pixel_scale == self.levels { return Some((self.input.clone(), None)) } let (width, height) = (self.width, self.height); // Distance between adjacent pixels for convolution (also // referred to as size of "hole"). let distance = 2_usize.pow(pixel_scale as u32); // Create new buffer to hold the computed data for this layer. let mut current_data = Array2::<f32>::zeros((height, width)); // Iterate over each pixel location in the 2D image for x in 0..width { for y in 0..height { // Set the current pixel in current layer to // the result of convolution on the current // pixel in input data. current_data[[y, x]] = self.compute_convoluted_pixel( distance, [x, y] ); } } // Create current layer by subtracting currently computed pixels // from previous layer let final_data = self.input.clone() - ¤t_data; // Set the input layer to equal the current computed layer so // that it can be used as the "previous layer" in next iteration. // This is also our residue data for each layer. self.input = current_data; // Return the current layer data as well as current level information. Some((final_data, Some(self.current_level))) } }من قصد دارم به این نکته اشاره کنم که در اینجا پتانسیل زیادی برای بهینه سازی عملکرد وجود دارد، اما این موضوع از حوصله این مقاله خارج است.
در نهایت خواهیم دید که چگونه می توانیم همه این لایه ها را برداریم و تصویر ورودی خود را بازسازی کنیم.
ترکیب مجدد
همانطور که قبلاً گفتم، بازسازی تصویری که با تبدیل A Trous تجزیه شده است به سادگی جمع کردن تمام لایه ها با هم است.
ما یک ویژگی را برای این تعریف می کنیم. اینکه چرا ما در اینجا به یک ویژگی نیاز داریم، باید زمانی که به اجرا نگاه میکنید، مشخص شود.
یک فایل جدید recompose.rs با محتویات زیر ایجاد کنید:
// recompose.rs use image::{DynamicImage, ImageBuffer, Luma}; use ndarray::Array2; pub trait RecomposableLayers: Iterator<Item = (Array2<f32>, Option<usize>)> { fn recompose_into_image( self, width: usize, height: usize, ) -> DynamicImage where Self: Sized, { // Create a result buffer to hold the pixel data for our output image. let mut result = Array2::<f32>::zeros((height, width)); // For each layer, add the layer data to current value of result buffer. for layer in self { result += &layer.0; } // Compute min and max pixel intensity values in the final data so that // we can perform a "rescale", which normalizes all pixel values to be // between the range of 0 & 1, as is expected by float 32 images. let min_pixel = result.iter().copied().reduce(f32::min).unwrap(); let max_pixel = result.iter().copied().reduce(f32::max).unwrap(); // Create a new `ImageBuffer`, which is a type provided by `image` crate to // serve as buffer for pixel data of an image. Here, we're creating a new // `Luma` ImageBuffer with pixel value of type `u16`. Luma just refers to // grayscale. let mut result_img: ImageBuffer<Luma<u16>, Vec<u16>> = ImageBuffer::new(width as u32, height as u32); // Pre-compute the denominator for scaling computation so that we don't // repeat this unnecessarily for every iteration. let rescale_ratio = max_pixel - min_pixel; // Iterate over all pixels in the `ImageBuffer` and fill it based on data // from the `result` buffer after rescaling the value. for (x, y, pixel) in result_img.enumerate_pixels_mut() { let intensity = result[(y as usize, x as usize)]; *pixel = Luma([((intensity - min_pixel) / rescale_ratio * u16::MAX as f32) as u16]); } // Convert the `ImageBuffer` into `DynamicImage` and return it DynamicImage::ImageLuma16(result_img) } } // Implement this trait for anything that implements the Iterator trait // with the given item type impl<T> RecomposableLayers for T where T: Iterator<Item = (Array2<f32>, Option<usize>)> {} اگر توجه نکردهاید، از آنجایی که ما این ویژگی را برای یک عمومی پیادهسازی میکنیم، با هر تکرارکننده مانند Filter ، Map و غیره کار میکند. اگر از یک ویژگی در اینجا استفاده نمیکردید، مجبور میشدید بارها و بارها همان چیز را برای هر نوع تکرارکننده داخلی پیادهسازی کنید، و کد شما با انواع شخص ثالث کار نمی کرد.
با استفاده از À Trous Transform
پس از همه اینها، بالاخره زمان آن رسیده است که پردازشی را که برای تصویر کهکشان به شما نشان دادم با نویز زیاد، بازتولید کنید. یک فایل main.rs جدید با محتویات زیر ایجاد کنید:
use image::{DynamicImage, ImageBuffer, Luma}; use atrous::recompose::RecomposableLayers; use atrous::transform::ATrousTransform; fn main() { // Open our noisy image let image = image::open("m33-noise-lum.jpg").unwrap(); // Create a new instance of the transform with 9 layers let transform = ATrousTransform::new(&image, 9); // Map over each layer transform.map(|(mut buffer, pixel_scale)| { // Create a new image buffer to hold the pixel data. This // will be populated from the raw buffer for this layer. let mut new_buffer = ImageBuffer::<Luma<u16>, Vec<u16>>::new(buffer.ncols() as u32, buffer.nrows() as u32); // Iterate over all pixels of the `ImageBuffer` to populate it. We also // convert from `f32` pixels to `u16` pixels. for (x, y, pixel) in new_buffer.enumerate_pixels_mut() { *pixel = Luma([(buffer[[y as usize, x as usize]] * u16::MAX as f32) as u16]) } // If the present layer is a small scale layer (< 3), // perform noise reduction if pixel_scale.is_some_and(|scale| scale < 3) { let mut image = DynamicImage::ImageLuma16(new_buffer).to_luma8(); // Bilateral filter is a de-noising filter. Apply it to the image. image = imageproc::filter::bilateral_filter(&image, 10, 10., 3.); // Modify the raw buffer to contain the updated pixel values after // filtering. for (x, y, pixel) in image.enumerate_pixels() { buffer[[y as usize, x as usize]] = pixel.0[0] as f32 / u8::MAX as f32; } // Return the updated buffer. (buffer, pixel_scale) } else { // Return the unmodified buffer for larger scale layers. (buffer, pixel_scale) } }) // Call the recomposition method on iterator .recompose_into_image(image.width() as usize, image.height() as usize) // Convert output to 8-bit grayscale image .to_luma8() // Save it to jpg file .save("noise-reduced.jpg") .unwrap() } همچنین باید یک وابستگی جدید ، imageproc را اضافه کنید ، که پیاده سازی های مفید پردازش تصویر را در بالای جعبه image فراهم می کند.
cargo add imageproc برای انجام این کار ، ما همچنین باید Cargo.toml خود را اصلاح کنیم تا صریحاً اهداف باینری و کتابخانه را تعریف کنیم:
// Cargo.toml [package] name = "atrous-rs" version = "0.1.0" edition = "2021" [[bin]] name = "atrous" path = "src/main.rs" [lib] name = "atrous" path = "src/lib.rs" # See more keys and their definitions at https://doc.rust-lang.org/cargo/reference/manifest.html [dependencies] image = "0.25.1" imageproc = "0.24.0" ndarray = "0.15.6" شما می توانید تصویر تست را از اینجا بارگیری کنید. آن را به فهرست اصلی پروژه خود منتقل کنید و cargo run --release . پس از اتمام ، باید یک پرونده جدید به عنوان noise-reduced.jpg روند ما به عنوان خروجی روند ما داشته باشید.
و حالا ما آن را در اختیار داریم.
بیشتر خواندن
اینها برخی از منابعی هستند که هنگام یادگیری این الگوریتم و نحوه استفاده از آن برای من بسیار مفید بودند. من هرکسی را که می خواهد درک فنی تر از الگوریتم را برای تحلیل این موارد بسیار تشویق می کنم.
تبدیل موجک گسسته شرت در PixInsight
تصویر نجومی و تجزیه و تحلیل داده ها توسط ژان لوک استارک و فونن مورتاغ
پردازش تصویر و سیگنال پراکنده: موجک ها و تجزیه و تحلیل چند مقیاس هندسی مرتبط توسط JL Starck ، F. Murtagh و J. Fadili
علاوه بر این ، من یک کتابخانه زنگ زدگی برای کار با Trous Transform ایجاد کرده ام. این نزدیک با آنچه من در اینجا به شما نشان داده ام مطابقت دارد ، اما از قبل برخی از ویژگی های اضافی نیز دارد و حتی بیشتر نیز خواهد داشت.
مواردی از قبیل دست زدن به تصاویر RGB و کار با هر 3 هسته مختلف از قبل اجرا شده است. همچنین منطق بهتری برای رسیدگی به شرایط مرزی دارد ، جایی که از تکنیک تاشو تصویر استفاده می کند.
من همچنین به زودی می خواهم در زمینه پیشرفت عملکرد برای همین کار کنم.
اگر می خواهید اطلاعات بیشتری کسب کنید یا در کتابخانه مشارکت کنید ، احساس راحتی کنید. مخزن را می توان در اینجا یافت: https://github.com/anshap1719/image-dwt
بسته بندی
امیدوارم تاکنون از سفر لذت برده باشید. اگر تکنیک های پردازش تصویر یا اجرای آنها در Rust چیزی است که به شما علاقه مند است ، پس بیشتر با ما در ارتباط باشید زیرا این موضوعاتی است که من دوست دارم درباره آنها بنویسم.
تا دفعه بعد ، برنامه نویسی مبارک و آرزو می کنم آسمان پاک کنید!



ارسال نظر