با پیشرفت زمینه های رمزنگاری و امنیت سایبری، رمزگذاری همومورفیک به عنوان یک فناوری پیشگامانه برجسته می شود.

این پتانسیل را دارد که همه چیز را در حریم خصوصی و امنیت داده ها تغییر دهد.

واقعا رمزگذاری همومورفیک چیست؟ چرا اینقدر مورد توجه قرار گرفته است؟ چگونه می تواند حریم خصوصی داده ها را افزایش دهد؟

اساساً، با رمزگذاری همومورفیک، می‌توانیم داده‌های رمزگذاری‌شده را بدون نیاز به رمزگشایی برای محاسبات پردازش کنیم.

این منجر به حفظ حریم خصوصی کامل در هر جایی که داده ها پردازش و ذخیره می شوند.

در این مقاله خواهید آموخت که چرا این نوع رمزگذاری انقلابی در حوزه امنیت ایجاد می کند. ما به سوالاتی مانند:

رمزگذاری همومورفیک چیست؟

رمزگذاری همومورفیک چگونه کار می کند؟

رمزگذاری هممورفیک در مقابل رمزگذاری سنتی - تفاوت چیست؟

کاربردهای رمزگذاری همومورفیک چیست؟

رمزگذاری همومورفیک چیست؟

بیایید از یک قیاس برای درک رمزگذاری همومورفیک استفاده کنیم.

صندوق گنج قفل شده ای را تصور کنید که در آن اشیاء با ارزش زیادی وجود دارد.

برای گفت ن یا حذف موارد، باید قفل سینه را باز کنید. این امر می تواند دزدی اقلام را هنگام باز کردن آن برای سارقان آسان تر کند.

در این قیاس، رمزگذاری سنتی این است.

رمزگذاری همومورفیک مانند داشتن یک دستکش جادویی است که به شما امکان می دهد بدون باز کردن قفل، موارد را از قفسه سینه اضافه یا حذف کنید.

به این ترتیب، خطر اینکه دزدها وسایل داخل صندوق گنج را به دست بیاورند را از بین می برید.

این اساساً همان کاری است که رمزگذاری هومورفیک با داده‌ها انجام می‌دهد: به ما اجازه می‌دهد تا بدون نیاز به رمزگشایی، عملیات روی داده‌های رمزگذاری شده انجام دهیم.

این با رمزگذاری سنتی امکان پذیر نیست. در آن صورت، ما باید داده هایی را که برای رمزگشایی نیاز داریم پردازش کنیم، هر محاسباتی لازم است را انجام دهیم و سپس دوباره داده ها را رمزگذاری کنیم.

با رمزگذاری homomorphic، امنیت هرگز به خطر نمی افتد.

رمزگذاری همومورفیک چگونه کار می کند؟

رمزگذاری همومورفیک به محاسبات اجازه می دهد تا روی داده های رمزگذاری شده عمل کنند - که به آن متن رمزی نیز می گویند.

این بدان معنی است که داده ها در حالی که رمزگذاری شده اند پردازش می شوند.

رمزگذاری همومورفیک محاسباتی را روی داده های رمزگذاری شده (متن رمز) انجام می دهد. اما محاسبات انجام شده در متن رمزگذاری شده نتایج رمزگذاری شده ای را ارائه می دهند.

وقتی این نتایج رمزگشایی می شوند، مشابه نتایجی هستند که اگر عملیات روی داده های اصلی و رمزگذاری نشده انجام می شد، به دست می آمد.

پس اساساً، رمزگذاری همومورفیک به عملیات روی داده‌های رمزگذاری‌شده اجازه می‌دهد تا همان نتایجی را به دست آورند که اگر روی داده‌های اصلی و رمزگشایی انجام می‌شدند.

چگونه این کار انجام می شود؟

رمزگذاری هممورفیک از الگوریتم های پیچیده ریاضی استفاده می کند که:

اعداد را برای مبهم کردن داده های اصلی تبدیل کنید و

همان عملیات را چه روی داده اصلی و چه روی این داده مبهم انجام دهید.

اساساً، شما همیشه روی داده های یکسانی به روشی مشابه کار می کنید، اما از دیدگاه های متفاوت.

پس می توانید با داده ها کار کنید و دقیقاً همان نتایجی را به دست آورید که گویی رمزگذاری نشده اند. اما از آنجایی که در واقع رمزگذاری شده است، داده ها همیشه محافظت می شوند!

به این ترتیب، هیچ کس نمی تواند آن را ببیند و ممکن است آن را بدزدد، که اجازه می دهد تا حریم خصوصی داده ها را حتی در محیط هایی که اعتماد آنها حداقل است، حفظ کند.

نمونه کد پایتون

ما قصد داریم از کتابخانه Pyfhel برای این مثال استفاده کنیم که می‌توانید در اینجا اطلاعات بیشتری درباره آن بخوانید.

در این کد قصد داریم دو عدد را به صورت رمزگذاری شده اضافه کنیم و نتیجه را ببینیم.

در اینجا کد کامل وجود دارد تا بتوانید به درستی درک کنید که رمزگذاری همومورف چگونه کار می کند:

 import numpy as np from Pyfhel import Pyfhel HE = Pyfhel() HE.contextGen(scheme='bfv', n=2**14, t_bits=20) HE.keyGen() integer1 = np.array([127], dtype=np.int64) integer2 = np.array([-57], dtype=np.int64) ctxt1 = HE.encryptInt(integer1) ctxt2 = HE.encryptInt(integer2) ctxtSum = ctxt1 + ctxt2 ctxtSub = ctxt1 - ctxt2 ctxtMul = ctxt1 * ctxt2 resSum = HE.decryptInt(ctxtSum) resSub = HE.decryptInt(ctxtSub) resMul = HE.decryptInt(ctxtMul)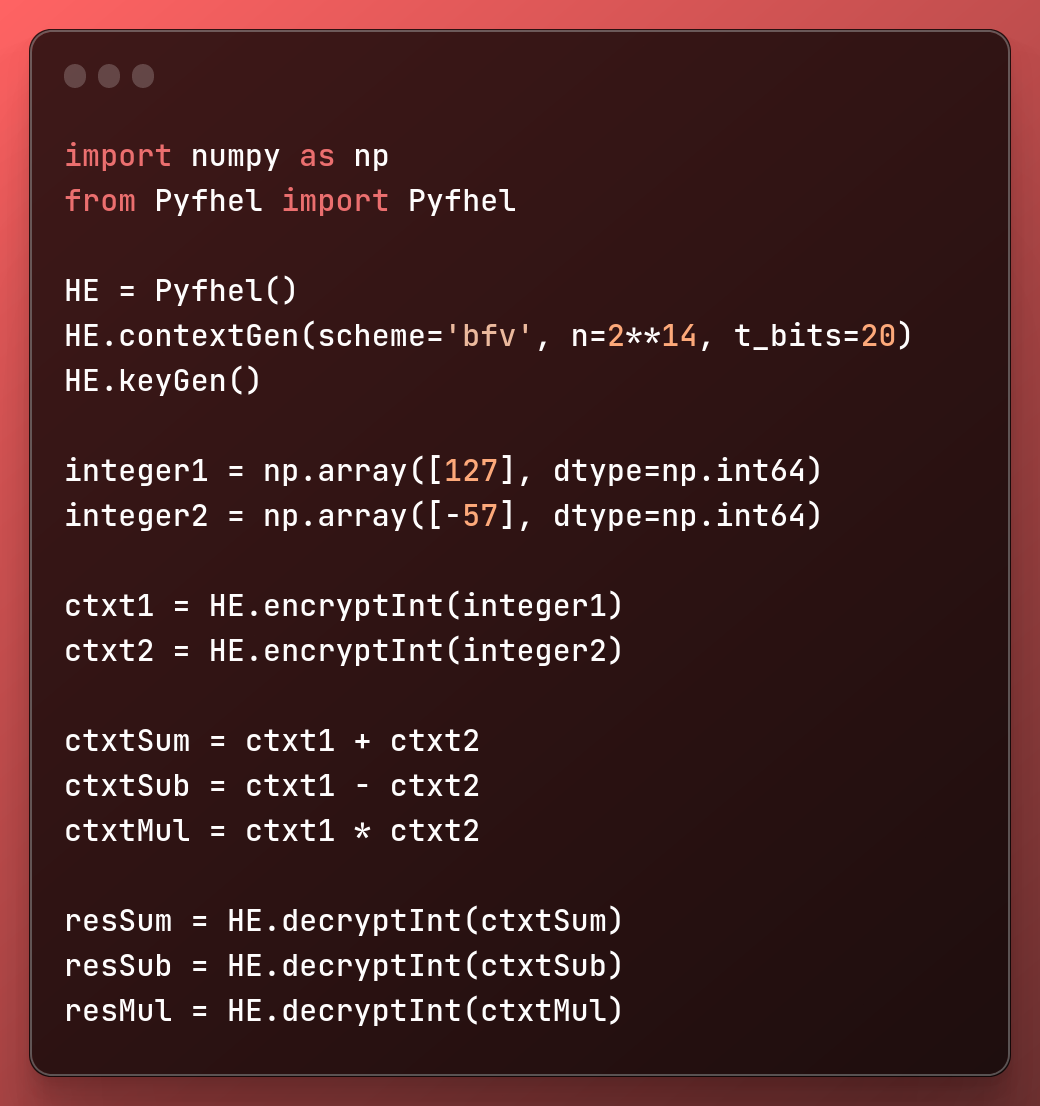

حال می‌خواهیم آن را خط به خط تجزیه کنیم:

ابتدا باید ماژول های لازم را وارد کنیم:

 import numpy as np from Pyfhel import Pyfhel

در اینجا، ما فقط ماژول های لازم را برای انجام محاسبات خود وارد می کنیم.

بعد، ما باید یک شی Pyfhel ایجاد کنیم و کلیدها را تولید کنیم:

 HE = Pyfhel() HE.contextGen(scheme='bfv', n=2**14, t_bits=20) HE.keyGen()

در خط اول یک شی پایتون Pyfhel مقداردهی اولیه می کنیم. در خط دوم رمزگذاری را با پارامترهای خاصی تنظیم می کنیم:

scheme='bfv' : ما از طرح رمزگذاری هممورفیک BFV (Brakerski/Fan-Vercauteren) استفاده می کنیم.

n=2**14 : درجه مدول چند جمله ای را تعریف می کند. درجه مدول چند جمله ای سطح امنیت رمزگذاری را با کارایی محاسباتی متعادل می کند. عدد بزرگتر رمزگذاری بهتری را ارائه می دهد اما به قیمت منابع محاسباتی بیشتر

t_bits=20 : اندازه بیت مدول متن ساده را تنظیم می کند. مقادیر اندازه بیت بزرگتر به شما امکان می دهد از اعداد بزرگتر استفاده کنید اما رمزگذاری را کمتر تمیز می کند

در خط سوم یک کلید عمومی و خصوصی تولید می کنیم

سپس دو عدد بدست می آوریم و آنها را رمزگذاری می کنیم:

 integer1 = np.array([127], dtype=np.int64) integer2 = np.array([-57], dtype=np.int64) ctxt1 = HE.encryptInt(integer1) ctxt2 = HE.encryptInt(integer2)

ما اعداد را در یک آرایه فقط با یک عدد نشان می دهیم و آنها را رمزگذاری می کنیم.

ما این اعداد را در یک آرایه نشان می دهیم و نه به این صورت که گویی متغیرها را اعلام می کنیم.

ما این کار را انجام می دهیم زیرا تابع encryptInt() تنها آرایه ای از اعداد صحیح با 64 بیت را به عنوان آرگومان می گیرد. از مستندات :

 encryptInt(self, int64_t[:] arr, PyCtxt ctxt=None)

اکنون عملیات را روی دو شماره در حالی که رمزگذاری شده است انجام خواهیم داد:

 ctxtSum = ctxt1 + ctxt2 ctxtSub = ctxt1 - ctxt2 ctxtMul = ctxt1 * ctxt2

و سپس اعداد را پس از عملیات رمزگشایی کنید، زمانی که رمزگذاری شدند:

 resSum = HE.decryptInt(ctxtSum) resSub = HE.decryptInt(ctxtSub) resMul = HE.decryptInt(ctxtMul)

که خروجی زیر را خواهد داشت:

 >>> [70 0 0 ... 0 0 0] >>> [184 0 0 ... 0 0 0] >>> [-7239 0 0 ... 0 0 0]

و اگر محاسبات عادی را بدون رمزگذاری انجام دهیم، می بینیم که مقادیر مطابقت دارند:

 integer1 = 127 integer2 = -57 print(integer1+integer2) print(integer1-integer2) print(integer1*integer2)

که موارد زیر را به دست می دهد:

 >>> 70 >>> 184 >>> -7239

همانطور که می بینید، اگر عملیات را روی داده ها در حالی که رمزگذاری شده است انجام دهیم، همان نتایجی را دریافت می کنیم که وقتی رمزگذاری نشده است انجام می دهیم.

رمزگذاری هم شکل در مقابل رمزگذاری سنتی - تفاوت چیست؟

در روش‌های رمزگذاری سنتی، قبل از هر نوع پردازش، داده‌ها باید رمزگشایی شوند.

در رمزگذاری همومورفیک، داده ها همیشه در حالت رمزگذاری شده استفاده می شوند.

رمزگذاری سنتی مانند یک پاکت امن است: برای خواندن یا اصلاح محتوا باید از آن خارج شود.

رمزگذاری همومورفیک مانند یک پاکت خاص است که امکان دستکاری محتوا را بدون نیاز به باز کردن آن برای خواندن یا تغییر می دهد.

کاربردهای رمزگذاری همومورفیک

کاربردهای عملی زیادی برای رمزگذاری همومورفیک وجود دارد.

در رایانش ابری، به کاربران اجازه می‌دهد تا داده‌ها را در فضای ابری پردازش کنند بدون اینکه هرگز آن‌ها را در معرض ارائه‌دهندگان خدمات ابری قرار دهند. به این ترتیب، اطلاعات حساس همیشه محرمانه باقی می مانند.

در مراقبت های بهداشتی، امکان تجزیه و تحلیل سوابق پزشکی رمزگذاری شده را بدون به خطر انداختن حریم خصوصی بیمار فراهم می کند. داده های سلامت بیمار همیشه محافظت می شود.

یکی دیگر از کاربردهای امیدوارکننده رمزگذاری همومورفیک در سیستم های رای گیری ایمن است. با استفاده از این نوع رمزگذاری، آرا به گونه ای شمارش می شود که هیچ کس نمی تواند ببیند که هر فرد به چه کسی رای داده است. این روند رای گیری را ایمن تر و خصوصی تر می کند.

این نمونه ها فقط نوک کوه یخ را نشان می دهند.

نتیجه

رمزگذاری هممورفیک یک تغییر پارادایم در نحوه مدیریت و پردازش داده های حساس است.

این فناوری و توسعه آن از آنجایی که نقض اطلاعات بیشتر و بیشتر در حال رخ دادن است، مهم است.

رمزگذاری هم شکل راهی به سوی ساده‌سازی مقررات حفظ حریم خصوصی داده‌ها ارائه می‌کند.

همچنین با ساده‌تر کردن حفاظت از داده‌های خصوصی و تشویق پیشرفت‌های امنیتی جدید، نوآوری بیشتری را ممکن می‌سازد.

خبرکاو