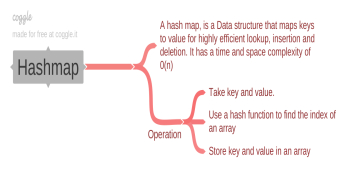
جدول هش یا نقشه هش، ساختار داده ای است که به نگاشت کلیدهای مقادیر برای عملیات بسیار کارآمد مانند عملیات جستجو، درج و حذف کمک می کند.

در این آموزش، موارد زیر را یاد خواهید گرفت:

پیچیدگی زمانی ثابت و خطی

چرا از نقشه هش استفاده کنیم؟

مواردی که باید هنگام نوشتن توابع هش در نظر بگیرید.

نحوه حل مشکل Two Sum در پی اچ پی و جاوا اسکریپت.

پیچیدگی زمان ثابت – O(1) چیست؟

O(1) نشان می دهد که زمان اجرای یک الگوریتم بدون توجه به اندازه ورودی ثابت است.

این بدان معناست که عملکرد الگوریتم به اندازه ورودی بستگی ندارد. یک مثال، دسترسی به فهرست یک آرایه است.

 <?php function constantTimeAlgorithm($arr) { echo $arr[0] . PHP_EOL; }

در اینجا یک مثال غیر کد برای نشان دادن مفهوم پیچیدگی زمانی ثابت آورده شده است:

تصور کنید که یک فایل از طریق یک شرکت هواپیمایی برای دوست خود ارسال می کنید، و شرکت هواپیمایی سیاستی دارد که براساس وزن بسته، هزینه را دریافت می کند.

حالا چه وزن پرونده شما 2 گرم باشد یا 20 کیلوگرم، زمان پردازش خطوط هوایی ثابت می ماند. این به این معنی است که مدت زمانی که طول می کشد تا شرکت هواپیمایی بسته شما را تحویل دهد به وزن پرونده بستگی ندارد – همیشه یکسان است.

به عبارت دیگر، زمان پردازش بدون توجه به حجم فایل ثابت است.

پیچیدگی زمانی خطی – O(n) چیست؟

O(n) نشان می دهد که زمان اجرای یک الگوریتم به صورت خطی با اندازه ورودی رشد می کند.

عملکرد الگوریتم به طور مستقیم با اندازه ورودی متناسب است. به عنوان مثال پیمایش حلقه for و عناصر چاپی است.

 <?php function linearTimeAlgorithm($arr) { foreach ($arr as $element) { echo $element . PHP_EOL; } }

در اینجا یک مثال غیر کد برای نشان دادن مفهوم پیچیدگی زمانی خطی آورده شده است:

استفاده از سرویس انتقال الکترونیکی را برای ارسال فایل به دوست خود در نظر بگیرید. در این سناریو زمان انتقال فایل به صورت خطی با حجم فایل افزایش می یابد.

به عنوان مثال، اگر انتقال یک فایل 100 مگابایتی 1 دقیقه طول بکشد، انتقال یک فایل 10 گیگابایتی با استفاده از همان سرویس تقریباً 100 دقیقه طول می کشد.

این رابطه خطی بین اندازه فایل و زمان انتقال آن نشان دهنده پیچیدگی زمانی خطی است. زمان انتقال فایل به طور متناسب یا خطی با اندازه ورودی یا فایل افزایش می یابد.

چرا از نقشه هش استفاده کنیم؟

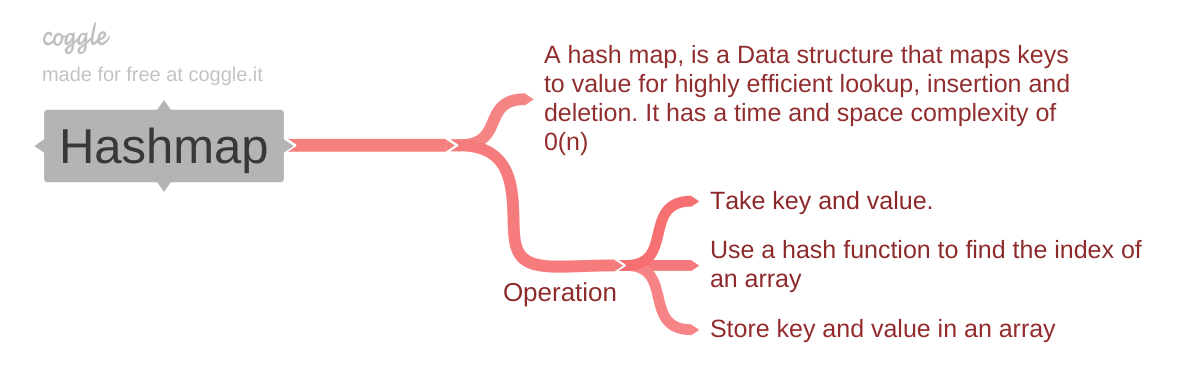
نقشه هش یک پیاده سازی مشخص از نوع داده انتزاعی است که به عنوان آرایه انجمنی شناخته می شود.

در یک نقشه هش، کلیدها برای تعیین شاخصی که مقادیر مربوطه در آن ذخیره می شوند، هش می شوند و امکان بازیابی و ذخیره موثر جفت های کلید-مقدار را فراهم می کند.

این پیاده‌سازی معمولاً زمان‌های دسترسی سریع را برای عملیات‌هایی مانند درج، حذف و جستجوی مقادیر بر اساس کلیدهای مرتبط با آنها فراهم می‌کند.

در زبان هایی مانند پی اچ پی یا جاوا اسکریپت، وقتی از یک آرایه انجمنی استفاده می کنید، اساسا از نقشه هش استفاده می کنید. آرایه های انجمنی آنها با استفاده از جداول هش در پشت صحنه پیاده سازی می شوند.

می‌توانید از رشته‌ها، اعداد صحیح یا دیگر انواع داده‌ها به‌عنوان کلید استفاده کنید، و مکانیسم هش‌سازی داخلی زبان به‌طور مؤثری این کلیدها را به مقادیر متناظرشان نگاشت می‌کند. علاوه بر این، جاوا اسکریپت شی Map را برای عملکردهای نقشه هش پیشرفته تر فراهم می کند.

پیچیدگی زمان و مکان برای نقشه هش

پیچیدگی زمان و مکان برای نقشه هش (یا جدول هش) لزوماً برای همه عملیات O(n) نیست. پیچیدگی زمانی معمول و مطلوب برای عملیات های اساسی مانند درج، جستجو و حذف در یک نقشه هش خوب طراحی شده به طور متوسط ​​O(1) است.

در اینجا یک تفکیک از پیچیدگی زمان و مکان برای یک نقشه هش آمده است:

پیچیدگی زمانی:

میانگین مورد:

درج (متوسط): O(1)

جستجو (متوسط): O(1)

حذف (متوسط): O(1)

بدترین حالت:

درج (بدترین): O(n)، که در آن n اندازه نقشه هش است. این زمانی اتفاق می‌افتد که برخوردهای هش زیادی وجود داشته باشد که منجر به کاوش خطی یا سایر استراتژی‌های حل تصادم می‌شود که ممکن است شامل عبور از کل نقشه هش باشد.

جستجو و حذف (بدترین): O(n)، به همان دلیل درج.

پیچیدگی فضا:

پیچیدگی فضا معمولاً O(n) است. جایی که n تعداد جفت های کلید-مقدار ذخیره شده در نقشه هش است. هر جفت کلید-مقدار فضای ثابتی را اشغال می کند و فضای مورد نیاز به صورت خطی با تعداد عناصر افزایش می یابد.

در تحلیل الگوریتم، نماد O(1) و O(n) کران های بالایی را در پیچیدگی زمانی یک الگوریتم نشان می دهد، جایی که n اندازه ورودی است.

عملیات

درج: جفت کلید-مقدار هش شده و از شاخص به دست آمده برای ذخیره مقدار در شکاف مربوطه استفاده می شود. اگر برخوردی رخ دهد، استراتژی حل برخورد اعمال می شود.

حذف: کلید برای یافتن نمایه هش می شود و مورد موجود در آن نمایه حذف می شود. تفکیک برخورد ممکن است ضروری باشد.

جستجو: کلید برای یافتن ایندکس هش می شود و مقدار آن شاخص برگردانده می شود. در صورت نیاز، وضوح برخورد ممکن است اعمال شود.

مواردی که باید هنگام ایجاد جداول هش در نظر بگیرید

هنگام ایجاد جداول هش، چندین ملاحظات مهم برای اطمینان از کارایی وجود دارد، از جمله محاسبه سریع کدهای هش و استراتژی های حل برخورد موثر.

محاسبات سریع

کدهای هش باید به سرعت محاسبه شوند تا از عملیات درج، جستجو و حذف کارآمد اطمینان حاصل شود. یک تابع هش خوب به سرعت محاسبه کد هش کمک می کند.

از برخورد جلوگیری کنید

تصادم زمانی اتفاق می افتد که دو یا چند کلید یک کد هش را تولید کنند. به عبارت دیگر، چندین کلید به یک شاخص آرایه نگاشت می شوند.

نحوه برخورد با برخوردها

نقشه های هش از تکنیک های تشخیص برخورد برای مقابله با برخوردها استفاده می کنند. استراتژی های رایج عبارتند از:

زنجیر زدن

برای مدیریت چندین مقدار با کد هش یکسان، زنجیره‌سازی شامل ذخیره‌سازی یک فهرست پیوندی یا دیگر ساختار داده در هر فهرست آرایه است. اگر برخوردی رخ دهد، جفت کلید-مقدار جدید به فهرست پیوندی در فهرست مربوطه اضافه می‌شود.

آدرس دهی را باز کنید

هنگامی که یک برخورد در جدول هش اتفاق می افتد، تکنیکی به نام آدرس دهی باز برای حل آن با جستجوی فضای باز بعدی استفاده می شود.

تنها کاری که انجام می دهد این است که آرایه را برای شکاف خالی بعدی که ترکیب کلید-مقدار را می توان در آن قرار داد جستجو کرد. روش هایی از جمله هش دوبل، کاوش درجه دوم و کاوش خطی اعمال می شود.

کاوش خطی: در کاوش خطی، الگوریتم به صورت خطی به شاخص بعدی در آرایه حرکت می کند تا در صورت وقوع برخورد، شکاف باز بعدی را پیدا کند.

کاوش درجه دوم: در این روش، یک الگوریتم از یک تابع درجه دوم برای یافتن شکاف بعدی که در دسترس می شود استفاده می کند.

Double Hashing: در هش دوبل، الگوریتم با استفاده از یک تابع هش ثانویه، اندازه گام بین پروب ها را محاسبه می کند.

به منظور کاهش احتمال برخورد، یک تابع هش خوب باید کدهای هش مجزا برای ورودی های مختلف تولید کند. با اطمینان از توزیع یکنواخت کدهای هش در محدوده مقادیر بالقوه، می توان از برخوردها جلوگیری کرد.

چگونه مسئله دو جمع را حل کنیم

مسئله Two Sum شامل یافتن تمام جفت عناصر در یک آرایه است که به یک مقدار هدف خاص جمع می شوند. حال بیایید به بیان مسئله نگاه کنیم.

بیان مسأله

با توجه به آرایه ای از nums و یک target صحیح، شاخص های دو عدد را به گونه ای برگردانید که به target جمع شوند.

مثال 1:

ورودی: nums = [3،2،4، 8]، هدف = 12

خروجی: [2، 3]

مثال 2:

ورودی: nums = [5,5]، هدف = 10

خروجی: [0,1]

راه حل

برای حل مسئله Two Sum می توانیم از جدول هش استفاده کنیم. ایده این است که از آرایه nums عبور کنید و برای هر عنصر تحلیل کنید که آیا مکمل (تفاوت بین عنصر هدف و عنصر فعلی) از قبل در جدول هش وجود دارد یا خیر. اگر اینطور باشد، ما یک جفت شاخص پیدا کرده ایم که عناصر آنها با هدف جمع می شوند.

در اینجا مراحلی وجود دارد که باید دنبال کنید:

برای نگهداری عناصر و شاخص های مربوطه آنها، پس از مقداردهی اولیه، یک جدول هش خالی ایجاد کنید.

به آرایه nums بروید.

محاسبه مکمل (هدف – عنصر فعلی) را برای هر عنصر انجام دهید.

تحلیل کنید که آیا مکمل قبلاً به جدول هش اضافه شده است. اگر بله، شاخص فعلی و شاخص ذخیره شده در جدول هش برای مکمل را برگردانید.

اگر مکمل در جدول هش نیست، عنصر فعلی و شاخص آن را در جدول هش ذخیره کنید.

اگر چنین جفتی در طول پیمایش یافت نشد، به این معنی است که راه حلی وجود ندارد.

راه حل کد پی اچ پی

 <?php function twoSum($nums, $target) { $hashTable = []; foreach ($nums as $i => $num) { $complement = $target - $num; if (array_key_exists($complement, $hashTable)) { // Found the pair, return the indices return [$hashTable[$complement], $i]; } // Store the current element in the hash table $hashTable[$num] = $i; } // No solution found return []; } // Example usage: $nums = [2, 7, 11, 5, 15, 30]; $target = 12; $result = twoSum($nums, $target); echo "Indices of the two numbers: [" . implode(", ", $result) . "]";

راه حل کد جاوا اسکریپت با استفاده از تابع map

 function twoSum(nums, target) { const hashTable = new Map(); for (const [index, num] of nums.entries()) { const complement = target - num; // Check if the complement is in the Map if (hashTable.has(complement)) { // Found the pair, return the indices return [hashTable.get(complement), index]; } // Store the current number and its index in the Map hashTable.set(num, index); } // No solution found return []; } // Example usage: const nums = [2, 7, 11, 5, 15, 30]; const target = 12; const result = twoSum(nums, target); console.log(`Indices of the two numbers that add up to ${target}: [${result.join(', ')}]`);

این رویکرد دارای پیچیدگی زمانی O(n) است زیرا ما یک بار در آرایه تکرار می کنیم. پیچیدگی فضا نیز به دلیل ذخیره عناصر در نقشه هش O(n) است.

منابع

جدول هش از ویکی پدیا

نقشه های هش در پایتون

نتیجه

در این مقاله، با نقشه‌های هش، مواردی که باید هنگام نوشتن توابع هش در نظر بگیرید و یک مشکل دنیای واقعی که شامل حل مسئله Two Sum است، آشنا شدید.

به یادگیری ادامه دهید و کدنویسی شاد باشید!

می توانید من را در لینکدین و توییتر پیدا کنید.

خبرکاو