چگونه تست های محک را برای توابع Golang بنویسیم
سلام گوفرز 👋
اجازه دهید با پرسیدن یک سوال از شما شروع کنم: چگونه عملکرد یک کد یا یک تابع را در Go آزمایش می کنید؟ خوب، شما می توانید از تست های معیار استفاده کنید.
در این آموزش، من به شما نشان خواهم داد که چگونه از یک ابزار محک عالی که در بسته آزمایشی Golang تعبیه شده است استفاده کنید.
برویم
تست های محک چیست؟
در Go، تستهای معیار برای اندازهگیری عملکرد (سرعت و استفاده از حافظه) توابع یا بلوکهای کد استفاده میشوند. این تستها بخشی از چارچوب تست Go هستند و در همان فایلهای تست واحد نوشته میشوند، اما آنها به طور خاص برای تجزیه و تحلیل عملکرد هستند.
مثال مورد استفاده: دنباله فیبوناچی
برای این مثال، من از دنباله کلاسیک فیبوناچی استفاده خواهم کرد که با این موارد تعیین می شود:
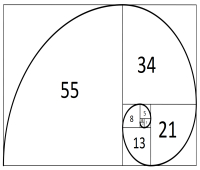
if (x < 2) F(0) = 1 F(2) = 2 else F(x) = F(x-1) + F(x-2) In practice, the sequence is: 1, 1, 2, 3, 5, 8, 13, etc.این دنباله مهم است زیرا در بخش های مختلف ریاضیات و طبیعت نیز ظاهر می شود، همانطور که در زیر نشان داده شده است:

راههای مختلفی برای پیادهسازی این کد وجود دارد، و من دو مورد از آنها را برای تست معیار خود انتخاب میکنم: روشهای بازگشتی و تکراری. هدف اصلی توابع ارائه یک موقعیت و برگرداندن عدد فیبوناچی در آن موقعیت است.
روش بازگشتی
// main.go func fibRecursive (n uint ) uint { if n <= 2 { return 1 } return fibRecursive(n -1 ) + fibRecursive(n -2 ) }تابع بالا یک پیاده سازی بازگشتی از محاسبه دنباله فیبوناچی است. اکنون به عنوان یک مبتدی در Go آن را گام به گام تجزیه و تحلیل می کنم.
تابع شما برای محاسبه اعداد فیبوناچی:
func fibRecursive (n uint ) uint { if n <= 2 { return 1 } return fibRecursive(n -1 ) + fibRecursive(n -2 ) }1. عملکرد:
func fibRecursive (n uint ) uint func : این کلمه کلیدی یک تابع را در Go تعریف می کند.
fibRecursive : این نام تابع است. به آن fibRecursive می گویند زیرا اعداد فیبوناچی را با استفاده از بازگشت محاسبه می کند.
n uint : تابع یک آرگومان منفرد، n را می گیرد که از نوع uint (یک عدد صحیح بدون علامت) است. این نشان دهنده موقعیت دنباله فیبوناچی است که قصد داریم محاسبه کنیم.
uint : تابع یک uint (عدد صحیح بدون علامت) را برمی گرداند زیرا اعداد فیبوناچی اعداد صحیح غیر منفی هستند.
2. مرحله پایه:
if n <= 2 { return 1 } دستور if تحلیل می کند که آیا n کمتر یا مساوی 2 باشد.
در دنباله فیبوناچی، اعداد 1 و 2 هر دو 1 هستند. پس ، اگر n 1 یا 2 باشد، تابع 1 را برمی گرداند.
این مرحله پایه نامیده می شود، و از عمیق شدن بی نهایت بازگشت جلوگیری می کند.
3. مرحله بازگشتی:
return fibRecursive(n -1 ) + fibRecursive(n -2 ) اگر n بزرگتر از 2 باشد، تابع دو بار خود را فراخوانی می کند:
fibRecursive(n-1) : این عدد فیبوناچی را برای موقعیت درست قبل از n محاسبه می کند.
fibRecursive(n-2) : این عدد فیبوناچی را برای دو موقعیت قبل از n محاسبه می کند.
سپس تابع این دو نتیجه را با هم جمع می کند، زیرا هر عدد فیبوناچی مجموع دو عدد قبلی است.
برای تئوری بیشتر در مورد بازگشت، این مقالات را تحلیل کنید.
روش تکراری
// main.go func fibIterative (position uint ) uint { slc := make ([] uint , position) slc[ 0 ] = 1 slc[ 1 ] = 1 if position <= 2 { return 1 } var result, i uint for i = 2 ; i < position; i++ { result = slc[i -1 ] + slc[i -2 ] slc[i] = result } return result }این کد یک رویکرد تکراری را برای محاسبه دنباله فیبوناچی در Go پیاده سازی می کند که با رویکرد بازگشتی متفاوت است. در اینجا خلاصه ای از نحوه عملکرد آن آمده است:
1. عملکرد:
func fibIterative (position uint ) uint func : این کلمه کلیدی یک تابع را در Go اعلام می کند.
fibIterative : نام تابع نشان می دهد که اعداد فیبوناچی را با استفاده از تکرار (حلقه) محاسبه می کند.
position uint : تابع یک آرگومان یعنی position می گیرد که یک عدد صحیح بدون علامت ( uint ) است. این نشان دهنده موقعیت دنباله فیبوناچی است که می خواهید محاسبه کنید.
uint : تابع یک عدد صحیح بدون علامت ( uint ) برمی گرداند که عدد فیبوناچی در موقعیت مشخص شده خواهد بود.
2. ایجاد یک Slice (ساختار آرایه مانند):
slc := make ([] uint , position) slc یک برش (آرایه پویا در Go) است که با طول position ایجاد می شود. این برش اعداد فیبوناچی را در هر شاخص ذخیره می کند.
3. مقادیر اولیه برای دنباله فیبوناچی:
slc[ 0 ] = 1 slc[ 1 ] = 1 دو عدد اول فیبوناچی هر دو 1 هستند، پس دو موقعیت اول در برش ( slc[0] و slc[1] ) روی 1 تنظیم میشوند.
4. بازگشت زودهنگام برای موقعیت های کوچک:
if position <= 2 { return 1 } اگر position ورودی 1 یا 2 باشد، تابع مستقیماً 1 برمی گرداند، زیرا دو عدد اول فیبوناچی همیشه 1 هستند.
5. حلقه تکراری:
var result, i uint for i = 2 ; i < position; i++ { result = slc[i -1 ] + slc[i -2 ] slc[i] = result } حلقه از i = 2 شروع می شود و تا رسیدن به position ادامه می یابد.
در هر تکرار، عدد فیبوناچی در شاخص i به عنوان مجموع دو عدد فیبوناچی قبلی ( slc[i-1] و slc[i-2] ) محاسبه میشود.
نتیجه هم در result و هم در slice slc[i] برای محاسبات آینده ذخیره می شود.
6. برگرداندن نتیجه:
return result پس از اتمام حلقه، result متغیر عدد فیبوناچی را در موقعیت مورد نظر نگه می دارد و تابع آن را برمی گرداند.
این یک روش کارآمدتر برای محاسبه اعداد فیبوناچی در مقایسه با بازگشتی است، به خصوص زمانی که position بزرگ است، زیرا محاسبات غیر ضروری را تکرار نمی کند و ما با استفاده از تست های معیار اثبات می کنیم . بیایید ثابت کنیم.
نحوه اجرای تست های بنچمارک
حالا برای تست های بنچمارک، چند تست بنویسیم. ابتدا باید یک فایل maintest.go ایجاد کنید. در آن، با استفاده از مستندات Golang در تستهای بنچمارک، میتوانید توابع مورد آزمایش را به صورت زیر ایجاد کنید:
// main_test.go // Benchmark for Iterative Function func BenchmarkFibIterative (b *testing.B) { for i := 0 ; i < bN; i++ { fibIterative( uint ( 10 )) } } // Benchmark for Recursive Function func BenchmarkFibRecursive (b *testing.B) { for i := 0 ; i < bN; i++ { fibRecursive( uint ( 10 )) } } بیایید تست را برای موقعیت 10 اجرا کنیم و سپس به طور مناسب افزایش دهیم. برای اجرای تست های بنچمارک، به سادگی دستور go test -bench=NameoftheFunction اجرا کنید.
اگر می خواهید در مورد این دستور بیشتر بدانید، اینجا را تحلیل کنید. بیایید عملکرد را برای موقعیت 10 تحلیل کنیم:
func BenchmarkFibIterative (b *testing.B) { for i := 0 ; i < bN; i++ { fibIterative( uint ( 10 )) } } go test -bench=BenchmarkFibIterative Results: cpu: Intel(R) Core(TM) i7 -7700 HQ CPU @ 2.80 GHz BenchmarkFibIterative -8 27715262 42.86 ns/op PASS ok playground 2.617 sبیایید با کمک این تصویر تجزیه و تحلیل کنیم:

با توجه به تصویر، ما 8 هسته برای آزمایش داریم و محدودیت زمانی نداریم (تا تکمیل خواهد بود). انجام این کار 27_715_262 تکرار و 1.651 ثانیه طول کشید.
func BenchmarkFibRecursive (b *testing.B) { for i := 0 ; i < bN; i++ { fibRecursive( uint ( 10 )) } } go test -bench=BenchmarkFibRecursive Results: cpu: Intel(R) Core(TM) i7 -7700 HQ CPU @ 2.80 GHz BenchmarkFibRecursive -8 6644950 174.3 ns/op PASS ok playground 1.819 sبا استفاده از همان تصویر برای تجزیه و تحلیل نتیجه، در این مورد 6_644_950 تکرار و 1.819 ثانیه طول کشید تا کار ما تکمیل شود:
| تابع فیبوناچی | موقعیت | تکرارها | زمان اجرا (ها) |
| تکراری | 10 | 27_715_262 | 1.651 |
| بازگشتی | 1 0 | 6_644_950 | 1.819 |
نتایج معیار نشان می دهد که رویکرد تکراری به طور قابل توجهی کارآمدتر از رویکرد بازگشتی برای محاسبه دنباله فیبوناچی است.
برای موقعیت 10، تابع تکراری تقریباً 27.7 میلیون تکرار را در 1.651 ثانیه انجام داد، در حالی که تابع بازگشتی تنها 6.6 میلیون تکرار را در 1.819 ثانیه انجام داد. روش تکراری هم از نظر تکرار و هم از نظر زمان از روش بازگشتی بهتر عمل کرد و کارایی آن را برجسته کرد.
برای اثبات بیشتر این موضوع، بیایید با موقعیت 40 (4 برابر مقدار قبلی) امتحان کنیم:
// Results for the Iterative Function cpu: Intel(R) Core(TM) i7 -7700 HQ CPU @ 2.80 GHz BenchmarkFibIterative -8 9904401 114.5 ns/op PASS ok playground 1.741 s // Results for the Recursive Function cpu: Intel(R) Core(TM) i7 -7700 HQ CPU @ 2.80 GHz BenchmarkFibRecursive -8 4 324133575 ns/op PASS ok playground 3.782 s| تابع فیبوناچی | موقعیت | تکرارها | زمان اجرا (ها) |
| تکراری | 40 | 9_904_401 | 1.741 |
| بازگشتی | 40 | 4 | 3.782 |
نتایج معیار به وضوح تفاوت کارایی بین رویکردهای تکراری و بازگشتی برای محاسبه دوباره فیبوناچی را برجسته میکند.
تابع تکراری تقریباً 9.9 میلیون تکرار را با میانگین زمان اجرای 114.5 نانوثانیه در هر عملیات تکمیل کرد و معیار را در 1.741 ثانیه به پایان رساند. در مقابل، تابع بازگشتی تنها 4 تکرار را با میانگین زمان اجرای 324،133،575 نانوثانیه در هر عملیات (بیش از 324 میلی ثانیه در هر تماس) تکمیل کرد، که 3.782 ثانیه طول کشید.
این نتایج نشان میدهد که رویکرد بازگشتی به دلیل فراخوانیهای مکرر تابع و محاسبات مجدد بسیار کارآمدتر است، و روش تکراری را هم در سرعت و هم در استفاده از منابع، بهویژه با افزایش اندازه ورودی، بسیار برتر میسازد.
فقط از روی کنجکاوی، موقعیت 60 را امتحان کردم و به معنای واقعی کلمه تست را خراب کرد:
// Results for the Iterative Function cpu: Intel(R) Core(TM) i7 -7700 HQ CPU @ 2.80 GHz BenchmarkFibIterative -8 7100899 160.9 ns/op // Results for the Recursive Function SIGQUIT: quit PC= 0x7ff81935f08e m= 0 sigcode= 0 goroutine 0 gp= 0x3bf1800 m= 0 mp= 0x3bf26a0 [idle]: runtime.pthread_cond_wait( 0x3bf2be0 , 0x3bf2ba0 ) ...نتیجه گیری
اگر کد تولید شما کندتر اجرا میشود یا بهطور غیرقابل پیشبینی کندتر است، میتوانید از این تکنیک، همراه با pprof یا ابزارهای دیگر از بسته آزمایشی داخلی، برای شناسایی و آزمایش محلهایی که کد شما عملکرد ضعیفی دارد استفاده کنید و روی نحوه بهینهسازی آن کار کنید.
به یاد داشته باشید: کدهایی که برای چشم زیبا هستند، لزوما کارایی بیشتری ندارند.
مرجع
توابع بازگشتی و تکراری به دنباله فیبوناچی در اینجا .
تست معیار در اینجا .
مشق شب
این مقاله توضیح می دهد که چرا برای برخی از اعداد کوچک، استراتژی بازگشتی بهتر است. آیا می توانید راه بهتری برای بهبود عملکرد بازگشتی پیدا کنید؟ (نکته: از برنامه نویسی پویا استفاده کنید).



ارسال نظر